|
STLdoc
STLdocumentation
|
|
STLdoc
STLdocumentation
|
Macros | |
| #define | _GLIBCXX_TR1_POLY_LAGUERRE_TCC 1 |
Functions | |
| namespace std | _GLIBCXX_VISIBILITY (default) |
This is an internal header file, included by other library headers. Do not attempt to use it directly. {tr1/cmath}
| #define _GLIBCXX_TR1_POLY_LAGUERRE_TCC 1 |
| namespace std _GLIBCXX_VISIBILITY | ( | default | ) |
This routine returns the associated Laguerre polynomial of order 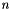 , degree
, degree 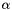 for large n. Abramowitz & Stegun, 13.5.21
for large n. Abramowitz & Stegun, 13.5.21
| __n | The order of the Laguerre function. |
| __alpha | The degree of the Laguerre function. |
| __x | The argument of the Laguerre function. |
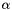 , and argument x.
, and argument x.This is from the GNU Scientific Library.
Evaluate the polynomial based on the confluent hypergeometric function in a safe way, with no restriction on the arguments.
The associated Laguerre function is defined by
![\[ L_n^\alpha(x) = \frac{(\alpha + 1)_n}{n!} _1F_1(-n; \alpha + 1; x) \]](form_164.png)
where 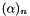 is the Pochhammer symbol and
is the Pochhammer symbol and 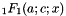 is the confluent hypergeometric function.
is the confluent hypergeometric function.
This function assumes x != 0.
This is from the GNU Scientific Library.
This routine returns the associated Laguerre polynomial of order 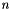 , degree
, degree 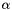 :
: 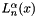 by recursion.
by recursion.
The associated Laguerre function is defined by
![\[ L_n^\alpha(x) = \frac{(\alpha + 1)_n}{n!} _1F_1(-n; \alpha + 1; x) \]](form_164.png)
where 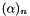 is the Pochhammer symbol and
is the Pochhammer symbol and 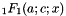 is the confluent hypergeometric function.
is the confluent hypergeometric function.
The associated Laguerre polynomial is defined for integral  by:
by:
![\[ L_n^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n + m}(x) \]](form_169.png)
where the Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_170.png)
| __n | The order of the Laguerre function. |
| __alpha | The degree of the Laguerre function. |
| __x | The argument of the Laguerre function. |
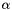 , and argument x.
, and argument x.This routine returns the associated Laguerre polynomial of order n, degree 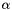 :
: 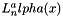 .
.
The associated Laguerre function is defined by
![\[ L_n^\alpha(x) = \frac{(\alpha + 1)_n}{n!} _1F_1(-n; \alpha + 1; x) \]](form_164.png)
where 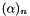 is the Pochhammer symbol and
is the Pochhammer symbol and 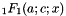 is the confluent hypergeometric function.
is the confluent hypergeometric function.
The associated Laguerre polynomial is defined for integral  by:
by:
![\[ L_n^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n + m}(x) \]](form_169.png)
where the Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_170.png)
| __n | The order of the Laguerre function. |
| __alpha | The degree of the Laguerre function. |
| __x | The argument of the Laguerre function. |
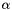 , and argument x.
, and argument x.This routine returns the associated Laguerre polynomial of order n, degree m: 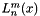 .
.
The associated Laguerre polynomial is defined for integral  by:
by:
![\[ L_n^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n + m}(x) \]](form_169.png)
where the Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_170.png)
| __n | The order of the Laguerre polynomial. |
| __m | The degree of the Laguerre polynomial. |
| __x | The argument of the Laguerre polynomial. |
This routine returns the Laguerre polynomial of order n: 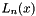 .
.
The Laguerre polynomial is defined by:
![\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} (x^ne^{-x}) \]](form_170.png)
| __n | The order of the Laguerre polynomial. |
| __x | The argument of the Laguerre polynomial. |
 1.8.6
1.8.6